New Scientist published an awesome article this week about nothing more complex than stacking blocks of wood (subscriber-only)… But, oh, how complex that task can be. It’s the combinatorial architecture of the well-balanced stack.
 [Image: The diagrammatic mathematics of a structural experiment by Mike Paterson and Uri Zwick, as reported in New Scientist].
[Image: The diagrammatic mathematics of a structural experiment by Mike Paterson and Uri Zwick, as reported in New Scientist].
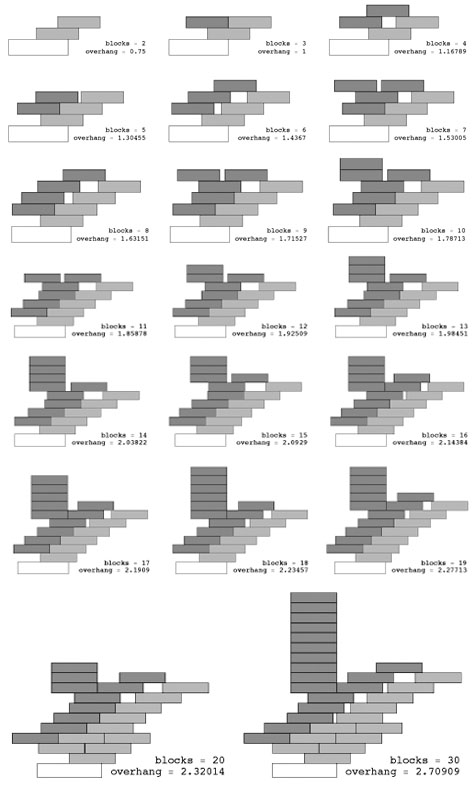
Computer scientists Mike Paterson and Uri Zwick have calculated new shapes and arrangements for the so-called “overhang problem,” by which one attempts to stack blocks outward from the edge of a table so that the blocks “overhang” as far as possible (before the stack collapses, or before you and your friends go out for more beer).
Strategically speaking, it turns out to be a matter of well-placed gaps, pressures, and weights.
 [Image: Two abstract stacks by Mike Paterson and Uri Zwick].
[Image: Two abstract stacks by Mike Paterson and Uri Zwick].
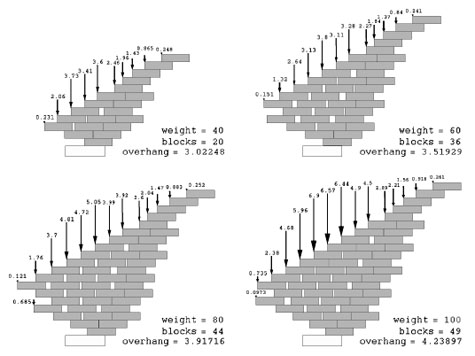
In two papers, available as PDFs (here and here), Paterson and Zwick write about balancing “harmonic stacks,” then stabilizing them, through “minute displacements” of space and weight within the stack structure.
A stack is said to be balanced if there exists a collection of forces acting between the blocks along their contact intervals, such that under this collection of forces, and the gravitational forces acting on them, all blocks are in equilibrium.
We read about loaded stacks and point weights, and “combinatorially distinct arrangements.”
 [Image: May the force stack with you; diagram by Mike Paterson and Uri Zwick].
[Image: May the force stack with you; diagram by Mike Paterson and Uri Zwick].
The authors advise that
one should, at least in principle, consider all possible combinatorial stack structures and for each of them find an optimal placement of the blocks. The combinatorial structure of a stack specifies the contacts between the blocks of the stack, i.e., which blocks rest on which, and in what order (from left to right), and which rest on the table.
They talk about parabolic stacks and spinal stacks (“A stack is spinal if its support set has just a single block at each level”), and about the spatial structure of brick walls, describing “well-behaved collections of forces that stabilize symmetric and asymmetric brick-wall stacks.”
 [Image: More stack madness by Mike Paterson and Uri Zwick].
[Image: More stack madness by Mike Paterson and Uri Zwick].
But what are the architectural implications of all this? Are there any?
Or, in this age of advanced materials, are basic formal considerations such as these reduced to useless tinkering? Why worry about well-balanced stacks, in other words, when you can just put some cantilevered I-beams up there and be done with it, making experiments like these instantaneously obsolete?
Superficially, these diagrams actually remind me of the demolition of London’s P&O Building this summer, in which the building was taken apart from the ground up, as if disappearing into the sky – thus exhibiting a rather unique variety of the overhang problem.
 [Image: London’s P&O Building gets demolished in reverse; via the Daily Mail. To see what brain death feels like, meanwhile, don’t miss the typically moronic comment thread over at Gizmodo, where brains go to die].
[Image: London’s P&O Building gets demolished in reverse; via the Daily Mail. To see what brain death feels like, meanwhile, don’t miss the typically moronic comment thread over at Gizmodo, where brains go to die].
So are there tens of thousands of overhang problems on display right now in the jungly tangles of rebar and steel that remain camouflaged behind the facades of architectural structures? Deep in the guts of engineered buildings the world over, are there interesting mathematical lessons to learn – provided we change how we look at walls and windows?
Is this the architectural equivalent of Rimbaud’s “systematic derangement of the senses” – to see mathematics and topology where others see mere elevators and unused attic floors? Inside our buildings, might there yet be more to find?
 [Image: View larger! Speculative demolition in Halle-Neustadt, via Nickzilla].
[Image: View larger! Speculative demolition in Halle-Neustadt, via Nickzilla].
We could actually attempt to answer that question.
Given billions of dollars, zero insurance liability, and a whole fleet of Komatsu wrecking machines, could you re-examine the overhang problem from an architectural standpoint, seeing how many floors and offices you can remove before a building tips over?
You’d make little Gordon Matta-Clark-esque incisions throughout the city – taking out whole floors and elevator shafts – cutting away at every building, one executive office suite at a time, till each building begins to tilt, warp, or list… at which point you’d stop, take a photograph, calculate something, then submit the image to a mathematics journal, thus winning the next Fields Medal for Applied Mathematics.
All of Manhattan a demolitionist research lab for extremely well-funded and aggressive mathematicians.
Could you then exhibit these removed pieces elsewhere – showing, say, the entire, fully intact eastern elevator shaft from the Empire State Building at the Guggenheim Abu Dhabi, forming some weird and abstract concrete pillar in the sky, whistling quietly in the desert wind, home to seagulls?
Modernist Totem Poles, you’d call it – and you could then steal the elevator shafts from the Transamerica Pyramid, the Sears Tower, the Chrysler Building, and Taipei 101.
In any case, does the stacking problem contain an architectural lesson? Read the original two papers featured in New Scientist to find out.
Awesome pictures!!
Rad.
i wish the starchitects had yearly jenga tourneys.
“…does the stacking problem contain an architectural lesson?”
Does a collapsing building make a sound in the city if there is no one to hear it?
I think this research does have big implications for architecture, if not for buildings (which would only happen if architects fail to take advantage of the results), then certainly for micro- (think nano- and meso-scale materials, self-assembling systems, etc.) and macro- (think arcologies) structures.
This would make a good game.
I see the blocks as 40′ shipping containers.